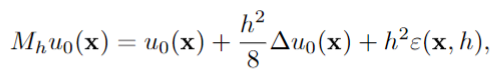Equation de la chaleur Equation donnée par : $$\begin{cases}\frac{\partial u}{\partial t}(t,\mathbf x)=\Delta u(t,\mathbf x)+g(\mathbf x)\\ u(0,\mathbf x)=u_0(\mathbf x)\end{cases}$$

• en traitement d'images, permet de modéliser les Convolutions avec des Gaussiennes
• on peut résoudre itérativement cette équation via : $$\begin{cases} u_0=u_0\\ u_{n+1}= u_n+\tau(\Delta u_n+g)\end{cases}$$
    
• pour que la méthode fonctionne, on doit avoir \(\tau\lt \frac14\)
• propriété importante : la Gaussienne \(G_t:\mathbf x\mapsto \frac1{\sqrt{4\pi}^N}e^{-\lvert\mathbf x\rvert/4t}\) satisfait l'équation de la chaleur \(\frac{\partial G_t}{\partial t}-\Delta G_t=0\)
    
• si \(g=0\), la méthode itérative peut alors s'écrire sous la forme \(u(t,\mathbf x)=(G_t*u_0)(\mathbf x)\)

Théorème d'existence et d'unicité de la solution

Existence et unicité des solutions de l'équation de la chaleur :

• \(u_0\in{\mathcal F}\) l'Ensemble des fonctions continues tendant vers une constante à l'infini
• \(u(t,\mathbf x):=(G_t*u_0)(\mathbf x)\)
• \(u(t,\infty):=u_0(\infty)\)
• \(u(0,\mathbf x):=u_0(\mathbf x)\)

$$\Huge\iff$$

• \(u\in\mathcal C^\infty\) et est bornée sur \(]0,+\infty[\times{\Bbb R}^N\)
• \(\mathbf x\mapsto u(t,\mathbf x)\) est dans \({\mathcal F}\), et ce \(\forall t\gt 0\)
• \(\forall t_0\gt 0\), \(u(t,\mathbf x)\overset{\text{unif} }{\underset{\mathbf x\to+\infty}\longrightarrow} u(\infty)\) pour tout \(t\leqslant t_0\)
• \(u(t,\mathbf x)\overset{\text{unif} }{\underset{t\to0}\longrightarrow}u_0(\mathbf x)\)
• \(u(t,\mathbf x)\) satisfait l'équation de la chaleur avec valeur initiale \(u_0\) : $$\frac{\partial u}{\partial t}=\Delta u\quad\text{ et }\quad u(0,\mathbf x)=u_0(\mathbf x)$$
• plus spécifiquement, $$\sup_{\mathbf x\in{\Bbb R}^N,t\geqslant0}\lvert u(t,\mathbf x)\rvert\leqslant\lVert u_0\rVert_{\mathcal F}$$
• inversement, étant donné \(u_0\in{\mathcal F}\), \(u(t,\mathbf x):=(G_t*u_0)(\mathbf x)\) est la seule solution \(\mathcal C^2\) bornée qui satisfait ces propriétés

Questions de cours

Il suffit de le montrer que pour \(\mathbf x\mapsto e^{-\lvert \mathbf x\rvert^2}\) puisqu'on peut en déduire le résultat pour les autres fonctions par récurrence.

Cela se fait simplement en dérivant.

START
Ω Basique (+inversé optionnel)
Recto: En quoi l'équation de la chaleur est-elle importante en traitement d'images ?
Verso: L'évolution d'une image \(u_0\) selon l'équation de la chaleur \(\frac{\partial u}{\partial t}=\Delta u\) peut modéliser la convolution d'une image avec une Gaussienne.
Bonus: Cela vient du lien entre le flou et le Laplacien discret :

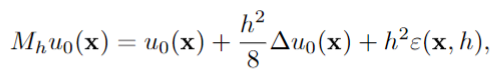
Carte inversée ?:
END